


Siguiente: Agradecimientos Subir: PRÓLOGO Anterior: Audiencia y objetivos Índice del Documento
Tras un primer capítulo introductorio, que quiere ser una
aproximación a la lógica en la
que presentamos de manera informal el objeto de la lógica y algunos
de los conceptos que consideramos más importantes (enunciado, argumento,
corrección, verdad, analiticidad, y relación de consecuencia lógica),
el contenido de este libro se ha organizado como sigue:
- Parte I. Lógica de Proposiciones.
- Capítulo 2. Semántica.
Se estudia la lógica de proposiciones
desde una perspectiva semántica. Se introduce el lenguaje formal de
la lógica de proposiciones: el lenguaje de las formas enunciativas.
Se define el
concepto de valoración que formaliza el proceso de atribución de
significado para las formas enunciativas. El concepto de
valoración nos permite precisar varios conceptos importantes y
demostrar algunas de sus propiedades: formas enunciativas
lógicamente equivalentes; formas enunciativas tautológicas y
el concepto de consecuencia lógica y forma argumentativa correcta.
- Capítulo 3.
Cálculo axiomático L y propiedades formales.
Se estudia la lógica de proposiciones desde una perspectiva
sintáctica.
Comenzamos definiendo el concepto de sistema formal e introducimos el
problema de la distinción entre lenguaje y metalenguaje,
al que damos gran relevancia durante todo el desarrollo de este libro.
Después, describimos el sistema formal axiomático L,
dedicando especial atención
al concepto de
deducción, ya que una de las finalidades del sistema formal es proporcionarnos
un método de cálculo que sirva para establecer la corrección de un argumento.
Puesto que deducir en el sistema formal L es difícil,
buscamos herramientas para facilitar esta tarea: el teorema de la deducción y
el teorema de intercambio.
Estudiamos las propiedades formales de la lógica de proposiciones,
centrándonos en la corrección, la consistencia, la completitud y la
decidibilidad; probamos que el sistema formal L posee todas estas
propiedades.
Para finalizar, se introduce el sistema de Kleene, como ejemplo de
sistema axiomático distinto del que nosotros empleamos.
- Capítulo 4. Cálculo de deducción natural.
Se presenta un sistema de deducción natural de tipo Gentzen que
flexibiliza el proceso de deducción en la propia lógica. Primero se describen
algunos de los métodos de prueba usados por los matemáticos, que tienen su
reflejo en las distintas reglas de inferencia básicas que componen nuestro sistema de
deducción natural.
El sistema que presentamos se caracteriza por hacer uso de un amplio conjunto de
conectivas lógicas, por poseer sólo reglas de inferencia (pero no
contener axiomas, contrariamente a lo que sucede con otras caracterizaciones
de los sistemas de deducción natural) y por tener un reducido
número de reglas para la construcción de una deducción.
Finalizamos el capítulo discutiendo la relación de nuestro sistema
de deducción natural con otros similares, como el cálculo de
secuentes. También demostramos la equivalencia deductiva entre el sistema L
y el sistema de deducción natural.
- Parte II. Lógica de Predicados.
- Capítulo 5. Semántica
En este capítulo se introduce el lenguaje de la lógica de predicados
y se estudian sus aspectos semánticos.
Primero se muestra la necesidad de introducir un lenguaje formal más rico,
en términos expresivos, que permita dar cuenta de los nombres, los functores,
los relatores y la cuantificación que es habitual en los lenguajes naturales.
Después se define el lenguaje formal de la lógica de predicados como un
sistema de símbolos desprovisto de toda significación e inmediatamente se
plantea el problema de su interpretación desde la perspectiva de la
teoría de modelos. Se precisan los conceptos de interpretación,
valoración, satisfacibilidad, verdad y validez. Estos conceptos nos permiten
ampliar el concepto de equivalencia lógica a la lógica de predicados.
También se demuestran diversas propiedades relativas a la noción de verdad y
validez.
Introducimos la noción de interpretación modelo, asociada a un
determinado tipo de fórmulas que llamamos `cerradas'. La noción de modelo es
determinante en la definición del concepto de consecuencia lógica. El teorema
de la deducción semántica pone en relación los conceptos de consecuencia
lógica y fórmula lógicamente válida. Para finalizar, se introduce el
concepto de independencia y la técnica de prueba de independencia,
que es útil para detectar cuándo una fórmula no es consecuencia lógica de
otro conjunto de fórmulas.
- Capítulo 6.
Cálculo axiomático
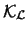 y propiedades formales.
y propiedades formales.
Estudiamos los aspectos sintácticos y las propiedades de la lógica de
predicados. Con este objetivo se introduce el sistema formal axiomático
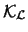 .
El sistema
.
El sistema 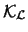 puede considerarse como una extensión del sistema
L con nuevos recursos expresivos y axiomas para poder tratar un
lenguaje más rico en el que tienen cabida las fórmulas cuantificadas.
Dado que deducir en el sistema formal
puede considerarse como una extensión del sistema
L con nuevos recursos expresivos y axiomas para poder tratar un
lenguaje más rico en el que tienen cabida las fórmulas cuantificadas.
Dado que deducir en el sistema formal 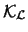 es tan difícil o más
que en el sistema L, también aquí buscamos herramientas para
facilitar la tarea de deducir. Probamos que tanto el teorema de la deducción
(con ciertas restricciones) como el teorema de intercambio siguen siendo válidos
en el sistema
es tan difícil o más
que en el sistema L, también aquí buscamos herramientas para
facilitar la tarea de deducir. Probamos que tanto el teorema de la deducción
(con ciertas restricciones) como el teorema de intercambio siguen siendo válidos
en el sistema 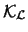 .
Estudiamos las propiedades formales de la lógica de predicados, comprobando que
el sistema formal
.
Estudiamos las propiedades formales de la lógica de predicados, comprobando que
el sistema formal 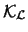 es: correcto, consistente y completo; pero indecidible
(si bien fragmentos de la lógica de predicados pueden probarse decidibles).
La indecidibilidad de la lógica de predicados impide su completa automatización
y sólo es posible implementar procedimientos de semidecisión, es decir,
que permiten comprobar la validez de una fórmula pero pueden no terminar, si la
fórmula es insatisfacible.
es: correcto, consistente y completo; pero indecidible
(si bien fragmentos de la lógica de predicados pueden probarse decidibles).
La indecidibilidad de la lógica de predicados impide su completa automatización
y sólo es posible implementar procedimientos de semidecisión, es decir,
que permiten comprobar la validez de una fórmula pero pueden no terminar, si la
fórmula es insatisfacible.
- Capítulo 7. Cálculo de deducción natural.
Aquí, se extiende el sistema de deducción natural del
Capítulo 4 con las reglas de inferencia apropiadas
para tratar la cuantificación.
Después de resumir los principales métodos de prueba usados por los
matemáticos cuando tratan con fórmulas cuantificadas, se introducen
las reglas de inferencia básicas para los cuantificadores:
un par de reglas de introducción/eliminación del cuantificador universal
y otro par de reglas de introducción/eliminación del cuantificador
existencial. También se introducen y justifican las reglas de inferencia derivadas y
se dan consejos prácticos para la resolución de argumentos cuando se usa
el sistema de deducción natural.
Para finalizar, se demuestra la equivalencia deductiva entre el sistema
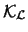 y el sistema de deducción natural.
y el sistema de deducción natural.
- Parte III. Extensiones de la Lógica Clásica
y Otras Lógicas.
- Capítulo 8.
Extensiones de la Lógica de Predicados.
En este capítulo
nos centramos en los sistemas de primer
orden con igualdad, que se abordan desde el punto de vista de los sistemas
axiomáticos y desde el punto de vista de los sistemas de deducción natural.
También estudiamos
la problemática que ocasiona la introducción de tipos y caracteríticas
de orden superior en el lenguaje de lógica de predicados. Comprobamos, mediante
numerosos ejemplos, que tanto el empleo de tipos como del orden superior
mejora la expresividad y el diseño de los lenguajes de programación.
- Capítulo 9. Otras Lógicas.
En la segunda parte del capítulo se caracterizan los principios
básicos sobre los que se fundamenta la lógica clásica (principio de
identidad, principio de bivalencia, principio de no contradicción,
principio del tercio excluso,...) y se estudian algunas de las llamadas
`lógicas desviadas' (lógicas multivalentes, lógica modal, lógica
intuicionista y lógica no monótona), indagando cómo se ven afectados
esos principios fundamentales de la lógica clásica por las nuevas
concepciones de la lógica.
También se comentan algunas de las aplicaciones de las lógicas no
clásicas.
Es conveniente notar que a lo largo del libro aparecen una serie de temas
recurrentes2que son de gran interés para
la formación del informático, como son: la distinción entre lenguaje y
metalenguaje; la técnica de definición por inducción; el conocimiento de
las diferentes técnicas de prueba y el problema de la representación del
conocimiento.
Dado que la representación del conocimiento es de singular importancia en el
campo de la Inteligencia Artificial, hemos querido prestarle suficiente
atención. En nuestro contexto, ese problema se concreta en el problema de
la traducción del lenguaje natural al lenguaje formal de la lógica.
En lugar de dedicar un capítulo ex professo a esta materia,
a lo largo del libro se proporcionan reglas prácticas y ejemplos que
permiten al lector adquirir pericia en el proceso de transformar frases del
lenguaje natural en fórmulas del lenguaje formal. Hemos preferido hacerlo
así tanto porque las técnicas son muy diversas como porque conviene
introducirlas desde el primer momento y agruparlas significaría
postergar el estudio de algunas de ellas hasta muy tarde.
Se ha dedicado el Apéndice A a la introducción de un
limitado número de notaciones y nociones matemáticas que es conveniente
que el lector conozca. Este apéndice puede usarse como un manual de referencia
rápido al que dirigirse sólo cuando se necesite.
Para finalizar, diremos que los contenidos enumerados en las dos primeras partes
se adaptan a una asignatura cuatrimestral (impartida en 15 semanas, con tres horas
de teoría y una de problemas por semana). Dichos contenidos pueden ampliarse
con apartados de la tercera parte hasta cubrir un semestre, dependiendo de la
profundidad y el detalle con el que se expliquen los mismos. En cualquier
circunstancia es recomendable incluir el Apartado 8.1 en un
primer curso de lógica. El resto de los contenidos presentados en la tercera
parte se consideran temas avanzados. También es recomendable que un curso
de estas características se complemente y prosiga con uno de programación
declarativa.



Siguiente: Agradecimientos Subir: PRÓLOGO Anterior: Audiencia y objetivos Índice del Documento
Pascual Julian Iranzo
2004-05-06
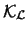 y propiedades formales.
y propiedades formales.
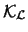 .
El sistema
.
El sistema 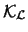 puede considerarse como una extensión del sistema
L con nuevos recursos expresivos y axiomas para poder tratar un
lenguaje más rico en el que tienen cabida las fórmulas cuantificadas.
Dado que deducir en el sistema formal
puede considerarse como una extensión del sistema
L con nuevos recursos expresivos y axiomas para poder tratar un
lenguaje más rico en el que tienen cabida las fórmulas cuantificadas.
Dado que deducir en el sistema formal 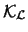 es tan difícil o más
que en el sistema L, también aquí buscamos herramientas para
facilitar la tarea de deducir. Probamos que tanto el teorema de la deducción
(con ciertas restricciones) como el teorema de intercambio siguen siendo válidos
en el sistema
es tan difícil o más
que en el sistema L, también aquí buscamos herramientas para
facilitar la tarea de deducir. Probamos que tanto el teorema de la deducción
(con ciertas restricciones) como el teorema de intercambio siguen siendo válidos
en el sistema 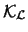 .
Estudiamos las propiedades formales de la lógica de predicados, comprobando que
el sistema formal
.
Estudiamos las propiedades formales de la lógica de predicados, comprobando que
el sistema formal 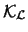 es: correcto, consistente y completo; pero indecidible
(si bien fragmentos de la lógica de predicados pueden probarse decidibles).
La indecidibilidad de la lógica de predicados impide su completa automatización
y sólo es posible implementar procedimientos de semidecisión, es decir,
que permiten comprobar la validez de una fórmula pero pueden no terminar, si la
fórmula es insatisfacible.
es: correcto, consistente y completo; pero indecidible
(si bien fragmentos de la lógica de predicados pueden probarse decidibles).
La indecidibilidad de la lógica de predicados impide su completa automatización
y sólo es posible implementar procedimientos de semidecisión, es decir,
que permiten comprobar la validez de una fórmula pero pueden no terminar, si la
fórmula es insatisfacible.
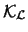 y el sistema de deducción natural.
y el sistema de deducción natural.