PRÓLOGO

La lógica simbólica o matemática estudia la lógica utilizando técnicas y nociones matemáticas. Al mismo tiempo ha contribuido a la fundamentación de las matemáticas. Aunque la lógica es una disciplina muy antigua, que hunde sus raíces en los filósofos griegos de la escuela de Megara, la escuela Estoica y Aristóteles, solamente se ha constituido en disciplina formal, es decir, en lógica simbólica (en adelante, simplemente `lógica'), a partir de la segunda mitad del siglo XIX, con los trabajos de A. De Morgan y G. Boole. Con el comienzo del segundo tercio del siglo XX la lógica se ha visto fertilizada por los nuevos problemas y técnicas surgidos alrededor de la informática (Ciencias de la Computación e Inteligencia Artificial).

La mayoría de los informáticos reconocen la íntima conexión existente entre la lógica y la informática, comparable en importancia a la relación existente entre el análisis matemático y la física. Desde el comienzo de su relación la lógica ha jugado diferentes papeles en el campo de la informática [3,4]:

1.

Como una fuente de lenguajes y sistemas para el razonamiento, debido a su capacidad deductiva. Se han empleado diferentes tipos de lógica para describir e implementar sistemas que razonan sobre un dominio en particular (e.g. en los campos de la teoría de la especificación y la inteligencia artificial). La lógica temporal, una clase de lógica modal, se ha empleado para razonar sobre sistemas que incorporan el tiempo como un parámetro principal. La lógica multimodal se ha empleado para razonar sobre sistemas concurrentes e indeterministas. La lógica multimodal también es útil en el campo de los lenguajes de especificación. La lógica no monótona se ha aplicado a una gran variedad de problemas que van desde la herencia de propiedades a las bases de datos deductivas y en todas aquellas áreas en las que es necesario emular razonamientos de sentido común o manejar informaciones imprecisas. La lógica borrosa también se ha utilizado para razonar sobre sistemas en los que el conocimiento es incierto.

2.

Como una fuente de herramientas y técnicas de análisis y fundamentación. La lógica se ha empleado como una herramienta para la representación del conocimiento y en otras muchas áreas de la inteligencia artifial. Desde el punto de vista de la fundamentación, la lógica se ha utilizado para proporcionar un modelo de cómputo. El 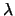$\lambda$-cálculo y la reducción de 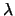$\lambda$-expresiones a formas normales, o bien la lógica de cláusulas de Horn y el principio de resolución SLD representan visiones idealizadas de la idea de cómputo. La lógica también se ha empleado para establecer una descripción formal del significado (semántica) de los lenguajes de programación y en la especificación y verificación formal de programas.

Vemos, pues, que pueden darse un gran número de razones para el estudio de la lógica aparte de ser una buena vacuna contra la obsolescencia tecnológica que siempre amenaza a los profesionales de la informática. Como se afirma en [1]: ``la lógica es particularmente importante porque es la base matemática del software''.