1.- Calcule la complejidad tanto de forma anal�tica como experimental de los siguientes m�todos de ordenaci�n: Burbuja, Inserci�n Directa, Selecci�n Directa, Mont�culo, Quicksort, Mergesort y m�todo de Shell. Los conjuntos de datos sobre los que se trabajar� ser�n de 10.000,� 100.000 y 1.000.000 elementos enteros. Recopile datos sobre distintas m�quinas.

2.- C�lculo del n-�simo t�rmino de la sucesi�n de Fibonacci.

a) Dise�e un algoritmo �Divide y Vencer�s� que calcule xⁿ con un coste O(n log n), en t�rminos del n�mero de multiplicaciones efectuadas.

b) Sea F la matriz 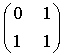. Considere el producto del vector (a b) por la matriz F. �Cu�l es el resultado cuando a y b son dos t�rminos consecutivos de la sucesi�n de Fibonacci.

c) Utilizando las ideas de los apartados anteriores, desarrolle un algoritmo �Divide y Vencer�s� para calcular el n-�simo t�rmino de la sucesi�n de Fibonacci. Calcule su coste en t�rminos del n�mero de operaciones aritm�ticas efectuadas.

3.- Juan, �el gorrilla�, ha sido contratado por el Casino DSAS3, sito en el n�mero 13 de la Calle del Percebe (en donde, hasta hace poco, se erig�a un antiguo bloque de pisos, habitado por exc�ntricos inquilinos). Su nuevo trabajo consiste en aparcar los coches de los clientes en el patio interior del inmueble. Dicho patio, reconvertido en parking de lujo, tiene forma de "T", de forma que se pueden aparcar coches en bater�a en el lado horizontal de dicha "T" y en l�nea o cord�n en el lado vertical de la "T", que sirve adem�s como pasillo de entrada al patio.

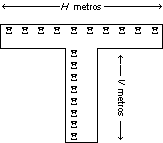
Ayude a Juan a encontrar la mejor forma de aparcar los coches, desarrollando un algoritmo que utilice una Heur�stica Voraz, de forma que consiga colocar la mayor cantidad de coches posibles y, de esta manera, pueda obtener la mayor suma de dinero en propinas.

Nota 1: En el patio solo cabe una hilera de coches en bater�a y otra a uno de los lados del pasillo de entrada.

Nota 2: Cada coche que llega al casino tiene unas dimensiones espec�ficas A_i x L_i, que ya incluyen el espacio de separaci�n necesario para poder aparcarlo.

4.- La Herencia. El abuelo Milbi Lletes est� en las �ltimas y sus dos nietos le est�n insistiendo constantemente para que le cuente qu� parte de su inmensa fortuna les deja. El abuelo por su parte no suelta prenda, pero s� les comenta que les dejar� una parte de su fortuna a partes iguales.

D�as m�s tarde el abuelo pasa a mejor vida y el Notario hace presencia en la mansi�n "Villa Billete". Una vez le�do el testamento y llegando a la parte en la que a los nietos se hace referencia, el notario lee: �Yo Milbi Lletes quiero dejar todo lo contenido en esta lista de bienes indivisibles, cada uno tasado seg�n la relaci�n que se adjunta, a mis dos nietos, Loqui Erotodo y Paca To. El reparto, que queda en manos del notario, debe ser lo m�s equitativo posible.�.

El notario viendo lo que tardar�a en cuadrar dicho problema, inteligente donde los haya, decidi� llamar a dos estudiantes de Ampliaci�n de la Programaci�n para resolverlo. �stos bien aleccionados en sus clases, le preguntaron que en caso de no ser exacta la divisi�n qu� deb�an hacer. El notario tras pensarlo decidi� que el mayor de los dos obtuviera la mayor parte.

Dise�e un algoritmo basado en Programaci�n Din�mica que realice el reparto de las pertenencias.

Proponga un conjunto [razonable] de condiciones bajo las cuales se puede construir un algoritmo de complejidad polinomial en funci�n del n�mero de bienes a repartir y el coste de estos bienes. Dise�e dicho algoritmo.

5.- Cruzar un Puente Estrecho y Peligroso. Tenemos un grupo de N personas que tienen que cruzar un puente por el que solo pueden ir en fila de a uno, y que adem�s, no soporta m�s que el peso de dos personas. Sabemos que el grupo solo dispone de una l�mpara para alumbrarse y que cada persona p tarda un tiempo t_p en cruzar el puente. Adem�s, cuando dos personas cruzan el puente tienen que llevar la l�mpara consigo, y el tiempo que emplean en cruzarlo es el mayor de las dos personas.

Dise�e un algoritmo que devuelva c�mo deben cruzar el puente para que el tiempo que empleen en ello sea m�nimo. Apl�quelo al caso de un grupo de cinco personas, cuyos tiempos en cruzar el puente de cada componente del grupo son: 1, 3, 6, 8 y 12 minutos.

6.- Backtracking. Resuelva el juego del Sudoku.

7.- Juego: En un grafo, cada v�rtice tiene un cierto valor, el bot�n. Dos ladrones, partiendo del mismo v�rtice y de forma alternativa, podr�n ir a cualquiera de los v�rtices adyacentes que a�n tengan bot�n. Si alguno no pudiera moverse, por no tener bot�n ninguno de sus adyacentes, pasar�a el turno al otro. El juego acaba cuando ninguno de los jugadores pueda moverse. Ganar� el que m�s dinero consiga.

Dise�e una funci�n que dada una posici�n del juego la eval�e y devuelva la decisi�n a tomar.